Using sdmvis in a simple SDM routine.
simple_use.RmdFor this vignette we will create a simple SDM to show how you can incorporate the functions of the sdmvis package in your routine of SDM. In fact, you can use sdmvis in any other spatial explicity analysis that would show the results similarly to an SDM/ENM.
Important note: we will follow the
dismopackage vignette of SDM (now available on rspatial.org), but in a more simplified way. I will focus on showing the functions, and not in followint the SDM best practices.
We will model the distribution of the sloth Bradypus variegatus. We will use the packages dismo, randomForest and sdmvis.
knitr::opts_chunk$set(warning = FALSE, message = FALSE)
# install.packages(c("dismo", "randomForest", "sdmvis"))
library(sdmvis)
#> Registered S3 methods overwritten by 'adehabitatMA':
#> method from
#> print.SpatialPixelsDataFrame sp
#> print.SpatialPixels sp
#> Registered S3 method overwritten by 'geojsonlint':
#> method from
#> print.location dplyr
library(dismo)
#> Loading required package: raster
#> Loading required package: sp
library(randomForest)
#> randomForest 4.6-14
#> Type rfNews() to see new features/changes/bug fixes.Fisrt of all, we will download occurrence data for this species using the gbif function on the dismo package. I will then plot it using the function pts_leaflet, from the sdmvis package.
# Download data
sp <- gbif(genus = "Bradypus", species = "variegatus")
# Get only lon/lat columns and remove NAs
sp <- sp[,c("lon", "lat")]
sp <- na.omit(sp)
# Plot using sdmvis package
pts_leaflet(sp)This ploting mode is better to visualize the occurrence points (we can zoom in!). For example, we see a point on the coast of Argentina that is clearly a problematic point. If you click on the point you can get the rownumber, what can help to solve the problem or further investigate it.
We will use some environmental data that is in the dismo package. First we will open the files and plot it using the var_leaflet function of the sdmvis package.
# we load the data on github
predictors <- stack(list.files(file.path(system.file(package="dismo"), 'ex'), pattern='grd$', full.names=TRUE )[1:8]) # here I will exclude one of the
# layers that is categorical
# now we plot using the var_leaflet, adding the points to see
var_leaflet(predictors, pts = sp)You can explore each one of the layers by clicking on the “stack” button on the right side of the Leaflet map. Note that when you move the mouse over the map, you get the lon/lat of the cursor (thanks to the functionality of the leafem package).
Now it would be good to also sort some pseudo-absence/background points. I will just randomly get some points over the environmental layers. I will also convert the presence points to 1 point per cell.
# Convert to 1 point per cell. Probably there is a simpler way to do that...
out.p <- raster::extract(predictors[[1]], sp[,1:2])
sp <- sp[!is.na(out.p),] # This is to ensure to get only points that fall in the
# environmental layer.
r <- raster(predictors[[1]])
r[cellFromXY(r, sp[,1:2])] <- 1
sp <- data.frame(rasterToPoints(r))
colnames(sp) <- c("x", "y", "pa")
# Sample random points 2x the quantity of presences
set.seed(2000)
backgr <- randomPoints(predictors, (nrow(sp)*2))
backgr <- data.frame(backgr)
backgr$pa <- 0
# We bind the two togheter
spdata <- rbind(sp, backgr)
# Plot again to see:
pts_leaflet(spdata)You can see that it now plots points with two different colors, one for presences and other for absences/background (you can change the colors).
Before moving to the SDM part, the var_leaflet function that we used before have a nice functionality that you can use to explore the environmental variables according to the points. It will extract the info from variables and produce some summary tables and plots in an html file. For getting this you just have to set varsummary = TRUE.
# For now it ONLY works with presence/absence data!
var_leaflet(predictors, pts = spdata, varsummary = TRUE)You will get something like that, but in a separate file (here I will just include the tables for the whole area and for the points, and one plot):
[[1]]
| bio1 | bio12 | bio16 | bio17 | bio5 | bio6 | bio7 | bio8 | |
|---|---|---|---|---|---|---|---|---|
| Min. | 122.0000 | 375.0 | 215.0000 | 4.0000 | 179.0000 | 49.0000 | 67.0 | 125.0000 |
| 1st Qu. | 239.5000 | 1694.0 | 690.0000 | 99.0000 | 299.5000 | 167.0000 | 110.0 | 240.0000 |
| Median | 254.0000 | 2248.0 | 877.0000 | 204.0000 | 315.0000 | 196.0000 | 118.0 | 254.0000 |
| Mean | 246.5964 | 2395.0 | 923.5455 | 260.4618 | 309.2036 | 184.7818 | 124.4 | 247.5964 |
| 3rd Qu. | 264.0000 | 2848.5 | 1093.0000 | 333.0000 | 325.0000 | 211.0000 | 138.5 | 263.0000 |
| Max. | 284.0000 | 7682.0 | 2458.0000 | 1496.0000 | 356.0000 | 228.0000 | 219.0 | 282.0000 |
[[2]]
| bio1 | bio12 | bio16 | bio17 | bio5 | bio6 | bio7 | bio8 | |
|---|---|---|---|---|---|---|---|---|
| Min. | -9.0000 | 2.000 | 1.0000 | 0.0000 | 61.0000 | -198.0000 | 70.00 | -24.0000 |
| 1st Qu. | 163.0000 | 765.750 | 316.2500 | 32.0000 | 300.2500 | 24.2500 | 130.00 | 196.0000 |
| Median | 229.0000 | 1327.000 | 539.5000 | 95.0000 | 320.0000 | 130.5000 | 177.00 | 247.0000 |
| Mean | 204.6018 | 1417.938 | 579.0073 | 151.1073 | 307.2727 | 103.4236 | 203.82 | 215.7091 |
| 3rd Qu. | 257.0000 | 1951.000 | 863.2500 | 242.7500 | 332.7500 | 187.7500 | 261.00 | 261.0000 |
| Max. | 285.0000 | 7024.000 | 2458.0000 | 1254.0000 | 422.0000 | 236.0000 | 444.00 | 312.0000 |
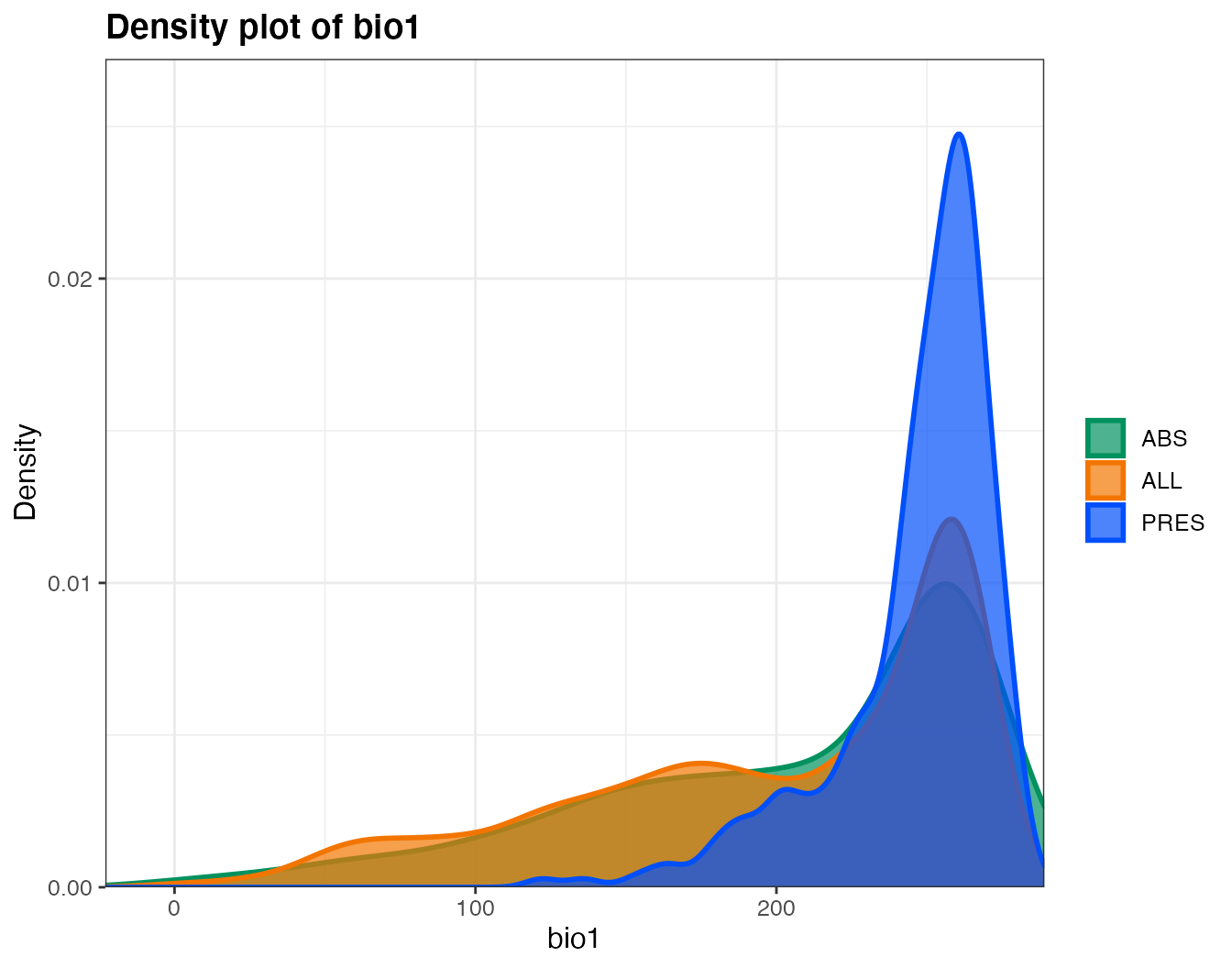
We will do a randomForest to produce an SDM. We will split the data to evaluate the model (we will separate 25% of the data).
## Extract the environmental data for each point
envdata <- extract(predictors, spdata[, 1:2])
envdata <- data.frame(cbind(spdata, envdata))
samp <- sample(nrow(envdata), round(0.75 * nrow(envdata)))
traindata <- envdata[samp,]
testdata <- envdata[-samp,]
## Fit a RandomForest model
# First we criate a model
model <- pa ~ bio1 + bio5 + bio6 + bio7 + bio8 + bio12 + bio16 + bio17
# Fit a random forest model
rf1 <- randomForest(model, data = traindata)
rf1
#>
#> Call:
#> randomForest(formula = model, data = traindata)
#> Type of random forest: regression
#> Number of trees: 500
#> No. of variables tried at each split: 2
#>
#> Mean of squared residuals: 0.1611983
#> % Var explained: 29.05
# Evaluate using the test data
erf <- dismo::evaluate(testdata[testdata[,3] == 1, 3:11],
testdata[testdata[,3] == 0, 3:11], rf1)
erf
#> class : ModelEvaluation
#> n presences : 59
#> n absences : 147
#> AUC : 0.8659057
#> cor : 0.5787027
#> max TPR+TNR at : 0.3179Now we can predict it to all the area and plot it using the sdm_leaflet function.
# Predict to the environment
pr <- predict(predictors, rf1)
# Plot using sdm_leaflet
sdm_leaflet(pr, mode = "continuous", pts = spdata, layernames = "RF")When we predict to a new environment, some areas may be out of the range used for training the model. In that case it’s important to assess in which areas the model will need to extrapolate1. One way to do that is using a MESS plot. In the var_leaflet you can easily get a MESS map to visualize using mess=TRUE:
var_leaflet(predictors, pts = spdata, mess = TRUE)
#> Obtaining MESS map using ecospat. This may take some minutes...we are interested in getting a binary map (i.e. thresholded). Before applying a certain threshold we can explore how different threshold values will look like. This can be helpfull in a sort of situations, as for example to decide, when you have two viable threshold options, which one is closer to what is expected to the species distribution (you should certainly chose the threshold based on methodological aspects, and not on what looks best; but, knowledge of the species biology can help you here).
This function can take longer to execute, depending on the number of thresholds.
# Lets see the model evaluation again
erf
#> class : ModelEvaluation
#> n presences : 59
#> n absences : 147
#> AUC : 0.8659057
#> cor : 0.5787027
#> max TPR+TNR at : 0.3179
#We get some thresholds here
thrs <- threshold(erf)
thrs
#> kappa spec_sens no_omission prevalence equal_sens_spec sensitivity
#> thresholds 0.3179 0.3179 0.1166333 0.2860667 0.3447333 0.2225619
# We can try two thresholds, one that maximizes the specificity+sensitivity
# and one for no omission (this second is usually a 'bad' one).
sdm_thresh(pr, thresh = c(thrs$spec_sens, thrs$no_omission),
tname = c("spec_sens", "no_omission"),
pts = spdata)Once we choose a threshold, we can make our binary map and plot it using the sdm_leaflet function, but with the "binary" mode. You can choose which palette to use, but here we will use the standard one.
binary <- calc(pr, function(x){
x[x < thrs$spec_sens] <- 0
x[x >= thrs$spec_sens] <- 1
x
})
sdm_leaflet(binary, mode = "bin", pts = spdata)You may want to see how the distribution of the species will be in the future. Here we will simulate an increase in some values for three of the variables (this is completely at random) and then predict the distribution for this new environment.
# We will increase the value of predictors at random
predictors.fut <- predictors
predictors.fut[[1]] <- predictors.fut[[1]] * 0.75
predictors.fut[[2]] <- predictors.fut[[2]] + 1.5
predictors.fut[[3]] <- predictors.fut[[3]] * 1.5
# Predict to the environment
pr.fut <- predict(predictors.fut, rf1)
binary.fut <- calc(pr.fut, function(x){
x[x < thrs$spec_sens] <- 0
x[x >= thrs$spec_sens] <- 1
x
})
# I will stack both the current and "future" to plot both
predictions <- stack(binary.fut, binary)
sdm_leaflet(predictions, mode = "bin", pts = spdata,
layernames = c("Future", "Current"))But we may also be interested in have a mapt that explicitly shows how the distribution will change. The simple way is to see the difference between the two rasters and then plot it using the "quad" mode on the sdm_leaflet package.
dif <- (binary.fut * 2) + binary
sdm_leaflet(dif, mode = "quad", pts = spdata,
layernames = c("Difference"))Finally, we may produce some spatial explicity error metric during our SDM routine. Here we will do a bootstrap analysis to see the coefficient of variation of the predictions when we sort new data points. We will run it only 30 times.
bootstrap <- pr
for (i in 2:30) {
btdata <- traindata[sample(1:nrow(traindata), size = nrow(traindata),
replace = T), ]
rfbt <- randomForest(model, data = btdata)
prbt <- predict(predictors, rfbt)
bootstrap <- stack(bootstrap, prbt)
}
m.mean <- calc(bootstrap, mean)
m.sd <- calc(bootstrap, sd)
boot.cv <- m.sd/m.meanWe can plot it using the sdm_highlight function and ask the function to highlight to us the places where there are the highest (or lowest) values for the coefficient of variation.
sdm_highlight(boot.cv, quantile = 0.75,
both.sides = TRUE, pts = spdata)sdmvis functions are also helpful to produce interactive reports/pages to show your results. Soon a vignette about this!